Here we find 4 functions: LDIV, LUDIV, LMOD, and LUMOD, and the standard variations: N_LDIV@, F_LDIV@, N_LUDIV@, F_LUDIV@, N_LMOD@, F_LMOD@, N_LUMOD@, F_LUMOD@

Like with PADD and PSUB we find multiple entrypoints to the same function:

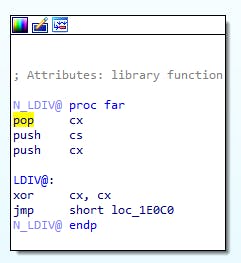
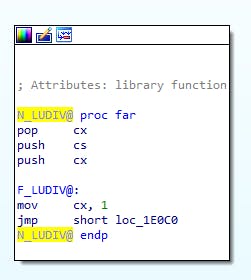
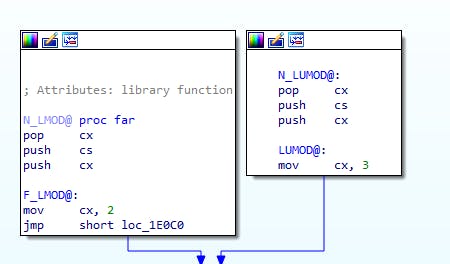
We see the same near/far pattern as with the others so I won't go into it here, but you can see it's a common pattern.

The first thing we notice is that they all set CX to something before carrying on:

• LDIV sets to 0
• LUDIV sets to 1
• LMOD sets to 2
• LUMOD sets to 3

In other words:

• bit 0 = 0: unsigned
• bit 0 = 1: signed
• bit 1 = 0: division
• bit 2 = 1: mod

Here's the start of the shared code:

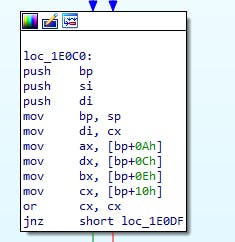
This is some standard prolog: save SP in BP, save SI/DI, keep CX (operation flags) in DI, then load our arguments. How does this get called then?

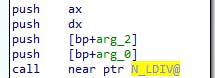
We can see it get called with two args next to each other, and DX:AX, so we could guess that we're dealing with 32-bit division here. We load these into DX:AX and CX:BX, then we do a zero-check on CX...

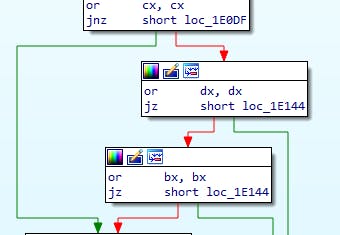
There's a shortcut branch which happens when:

• CX==0 and DX==0
• CX==0 and BX==0

Let's take a peek to where it goes:

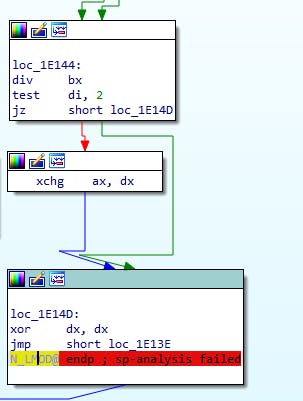
If either of these cases is true we execute DIV BX, which is the same as

DX = AX % BX // remainder
AX = AX / BX // division

Then if bit one on DI is set then we return DX (mod), otherwise we return AX.

So a couple of things here:

• DX:AX is our dividend (the big number)
• CX:BX is the divisor (the number we divide into)
• If CX==0 and DX==0 then we're doing 0:AX / 0:BX and we can do that with a 16-bit DIV
• IF CX==0 and BX==0 then we're doing DX:AX/0 and we just want to get the "divide by zero" error

So by skipping the main body and following a nice shortcut branch we actually learned a lot about what's going on, here are the comments for the chunk up top again:

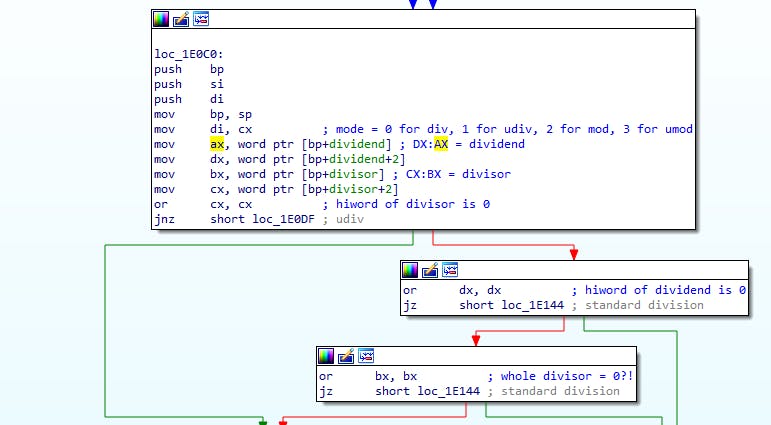
Let's carry on down the main path:

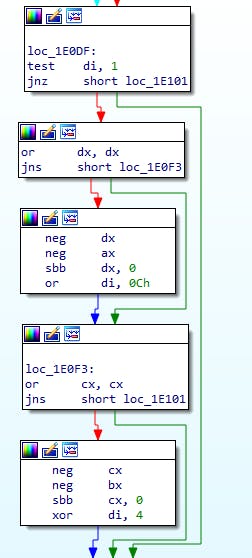
So from the top:

test    di, 1
jnz     short loc_1E101

Bit 0 is if we're doing signed division - if not then skip this entire chunk. We're going to do something to handle negative numbers then?

or      dx, dx
jns     short loc_1E0F3

Check the sign bit on DX and skip if not set (if DX is positive). If DX is negative though:

neg     dx
neg     ax
sbb     dx, 0
or      di, 0Ch

This is a bit convoluted. The NEG instruction does a NOT then adds 1 to give us the two's complement. We do this to both DX and AX, then we do a SBB... why is this?

The problem is that the NEG on AX is fine (NOT and then +1), but on DX we end up with an extra +1 that doesn't make sense (compare if we did this in EAX, it would only do the +1 once).

In other words, if we have 10101010:10101010 it'll do this:

// original 10101010:10101010
not
// 01010101:01010101
inc
// 01010110:01010110

If we did this with the numbers together we'd get this:

// original 1010101010101010
not
// 0101010101010101
inc
// 0101010101010110

(yes we're using 16-bits here but the concept is the same)

This is where the next instruction comes in: SBB DX,0. The NEG instruction is defined to set CF unless the number is 0. In other words, we're basically doing DEC DX after to cancel it out... unless AX is 0. Here's how this plays out:

// original 1010101000000000
not
// 0101010111111111
inc
// 0101011000000000

The one edge case with AX=0 gets inverted to 0xFFFF, and incrementing it by 1 passes the 1 all the way to the top and gives us a carry/overflow. That means the NEG doesn't set CF, so our SBB command does nothing. Kinda crazy, but the system works :)

We then OR DI with 0x0C, or 1100 in binary - it sets bits 2 and 3.

The next part is the same but on CX:BX, and then we XOR 0x04 onto DI (bit 2). This gives us the following state for DI:

• bit 0: unset=div, set=mod
• bit 1: unset=signed, set=unsigned
• bit 2: divisor and dividend have the same sign (both positive or both negative)
• bit 3: divisor is negative (no information on dividend)

Now it's time for the fun part:

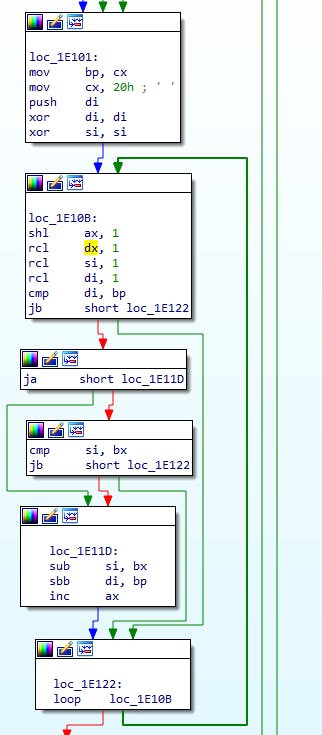
This part had me stumped for a bit, but going through step by step will get us there. Here's the start:

mov     bp, cx

Divisor is now BP:BX (so we're doing DX:AX / BP:BX)

mov     cx, 20h ; ' '

Setting CX to 0x20 (32), looks like we're looping over something 32 times, and we are doing 32-bit division...

push    di
xor     di, di
xor     si, si

We're saving DI for later (so we don't care about those bits we just set right now), and clearing DI/SI to 0.

That was the init for the loop. Let's jump and see what we do each of the 32 times:

shl     ax, 1
rcl     dx, 1
rcl     si, 1
rcl     di, 1

This treats DI:SI:DX:AX like one big 64 bit number, and does a SHL on the whole thing. We could also see it as follows:

DI:SI = DI:SI << 1
DI:SI += HIGHBIT(DX:AX)
DX:AX = DX:AX << 1

So each time through the loop we copy a bit from DX:AX into DI:SI and shift it all up, 32 times for the 32-bit number

cmp     di, bp
jb      short loc_1E122
ja      short loc_1E11D

Remember the divisor is BP:BX, so we're comparing the high word of BP:BX with the high word of DI:SI. If DI < BP then we continue the loop, if DI > BP then we do the operation at loc_1E11D.

cmp     si, bx
jb      short loc_1E122

If we got here then the high words are equal, and we now compare the low word of BP:BX with DI:SI - if SI<BX then DI:SI<BP:BX and we continue with the loop

loc_1E11D:
sub     si, bx
sbb     di, bp
inc     ax

We make it here if DI:SI > BP:BX. What does that mean?

Long division

You probably covered this at school, but here's a primer anyway. If we want to divide numbers like 12345 / 57 we can do it like this:

// put a 57 on the front
0012345
5700000
// 5700000 > 12345 so put a 0
012345
570000
0
// 570000 > 12345 so put a 0
12345
57000
00
// 57000 > 12345 so put a 0
12345
5700
000
// 5700 < 12345, 2x5700 < 12345 but 3x5700 > 12345 so we put a 2 and subtract 12345 - 2x5700
945
570
0002
// 570 < 945. 2x57 > 945, so put a 1 and subtract 570
375
57
00021
// 57 x6 = 342 < 375, so put a 6 and subtract 342
33
DONE
000216

So 12345 / 57 = 216 remainder 33. To check: 216 x 57 = 12312, and 12312 + 33 = 12345.

This is actually easier in binary, because we don't need to count how many times the number divides in, we just put a 1 if it's smaller (and then subtract), or a 0 if it's bigger and keep going. We can do the same thing in binary:

11000000111001 // 12345 in binary
110000 // top 6 bits of 12345, rest are 00111001
111001// 57 in binary with a lot of left shifts
0
// bottom > top so leave a 0
1100000 // top 7 bits, rest are 0111001
111001
01
// top > bottom so leave a 1, 1100000-111001 = 100111
1001110 // add next bit, rest are 111001
111001
011
// top > bottom so leave a 1, 1001110 - 111001 = 10101
101011 // add next bit, rest are 11001
111001
0110
// top < bottom so leave a 0
1010111 // add next bit, rest are 1001
111001
01101
// top > bottom so leave a 1, 1010111 - 111001 = 11110
111101 // add next bit, rest are 001
111001
011011
// top > bottom so leave a 1, 111101 - 111001 = 100
1000 // add next bit, rest are 01
111001
0110110
// top < bottom
10000 // add next bit, rest is 1
111001
01101100
// top < bottom
100001 // all bits gone
111001
011011000
// top < bottom
// answer is 011011000 remainder 100001

011011000 = 216 in decimal 100001 = 33 in decimal

so we can see this works. As we saw, we do SUB SI,BX to subtract the bottom, then with the CF we do SBB DI,BP, and then we increment AX. We know we're shifting 32 bits, and that means DX:AX empties out as we shift, which means we can actually reuse DX:AX for our answer as we go along, and the remainder ends up in DI:SI. Pretty neat.

Once we're done with the loop we get this:

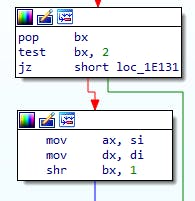
As with the short part, we check if this was DIV or MOD, and if it's a MOD then we save the remainder into DX:AX, otherwise we leave the quotient in DX:AX.

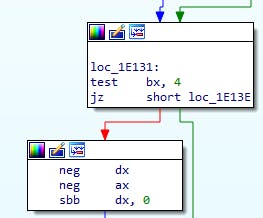
Testing bit 3 which checks if both dividend and divisor are the same sign. If they are different signs then we negate the answer, and then we're done.

So in summary, this function does the following:

• If the high 16 bits aren't used (or the divisor is 0) then do a normal DIV opcode
• If the high 16 bits are used then manually make both dividend and divisor positive, manually do binary long division to 32 bits, and then make the answer negative if one of the dividend or divisor was negative
• Return the quotient if we were doing division, otherwise return the remainder

Happy reversing!