These two are both intertwined so it makes sense to analyse them together:

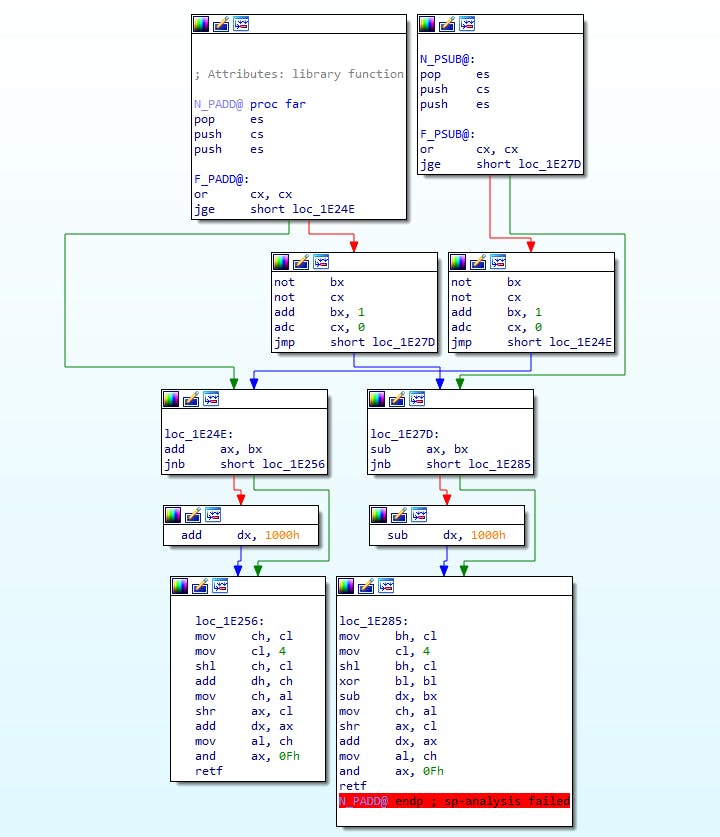
We can see a few variations on names at the top here: N_PADD@ and F_PADD@ for PADD, and N_PSUB@ and F_PSUB@ respectively. The prolog for the near versions is the same; it pops the return offset, pushes CS and then pushes the return offset back so it doesn't matter whether the call is a near or far call, we can always make a successful far return.

It's also useful to look how this is called:

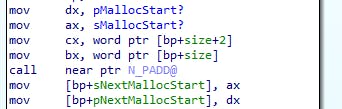
So it looks like we're taking DX:AX and CX:BX as arguments, and the result is returned in DX:AX. Let's start going through the code:

or      cx, cx
jge     short loc_1E24E

What the hell is this? The JGE instruction jumps if SF = OF. So we need to know what SF is, what OF is, and then whether they're equal. Looking closer at the OR instruction, we see it clears OF and sets SF to the high bit of the result. So we know that OF = 0, so we'll make the jump if SF = 0, or if CX is a positive number. There's another opcode JNS that could work here but it's all the same - we jump if CX is positive (and likely, if CX:BX is positive). Let's follow this branch:

loc_1E24E:
add     ax, bx
jnb     short loc_1E256

We're returning the result in DX:AX so it makes sense to add BX into AX. We know CX:BX is positive, so we start by adding the lower word. JNB jumps if CF = 0 (no carry), so let's see what we do with the carry:

add     dx, 1000h
loc_1E256:

This is fun. If DX:AX was a 32-bit value we'd be adding 1 to DX, but we're adding 0x1000 instead. That makes me think that DX:AX is a segment:offset pair and we're adding to that. Let's look further:

mov     ch, cl
mov     cl, 4
shl     ch, cl

We destroy CH here! We then shift CL left by 4 bits, so we destroy the top 4 bits of CL too. This makes sense if CX:BX is a 32-bit number, and if we're adding this to a segment:offset pair then the bottom 20 bits (all of BX plus the bottom 4 bits of CL) make sense to add. In other words, if CX:BX was 000a:bcde, we now have CH = a0.

add     dh, ch

Remember that 32-bit location 000abcde can be converted to segment:offset a000:bcde (among others). We added the lower part (bcde) to AX already, carried the 1, and now we're adding the top 4 bits to DX. DX:AX now holds the final segment:offset, but there's more code to go:

mov     ch, al
shr     ax, cl
add     dx, ax

We're saving the low byte of DX:AX, shifting AX right by 4 bits, then adding onto DX. What does this mean? It bumps the segment part to the highest value.

mov     al, ch
and     ax, 0Fh

Then we put the low byte in AL and mask it so we have the largest segment possible, and the lowest offset possible, while still pointing to the same point in memory.

In other words, this branch does the following:

// add the amount to the segment:offset
offset += lowword;
if(carry)
  segment += 0x1000;
segment += (hiword & 0x0F) * 0x1000;
// adjust segment:offset
segment += offset >> 4;
offset = offset & 0x0F;

The segment arithmetic is always hard to follow, but this is the basic idea of what happens there.

We only have 3 more branches to go here :) Let's take a quick look at the corresponding PSUB that gets us here:

or      cx, cx
jge     short loc_1E27D
not     bx
not     cx
add     bx, 1
adc     cx, 0
jmp     short loc_1E24E

If CX:BX is negative then we bit flip CX:BX, increment BX by 1, and then load the carry into CX. The reason they use the ADD command is that INC doesn't change CF so the following ADC wouldn't carry the 1. Why do we do this? This is what we call "two's complement" and this is just gives us the negative value, in other words:

CX:BX = -CX:BX

So if we're subtracting a negative number, this is the same as adding a positive number, e.g. 5 - -3 is the same as 5 + 3 so we'll use the addition path. The opposite is true on the addition path btw, if we're adding a negative number we'll just negate it and go down the subtraction path.

Anyway, let's see what the subtraction path does:

loc_1E27D:
sub     ax, bx
jnb     short loc_1E285
sub     dx, 1000h
loc_1E285:

This is the opposite of the addition path, we do AX - BX and then carry the 1 by subtracting 1000 from DX. Note that this can go negative if we have a weird segment:offset pair like 0000:F000 that could be better phrased as 0F00:0000.

mov     bh, cl
mov     cl, 4
shl     bh, cl

Same as above, if BX:CX was 000a:bcde we now have BH=a0

xor     bl, bl
sub     dx, bx

This is actually the same as above but for some reason they've done DX - BX instead of DH - BH - it does the same thing when BL is 0

mov     ch, al
shr     ax, cl
add     dx, ax
mov     al, ch
and     ax, 0Fh

And apart from the weirdness with BX this is the same segment:offset adjusting code from above.

I've used this signature for IDA: __int32 __usercall __far N_PADD_@<dx:ax>(int sSource@<dx>, void near* pSource@<ax>, __int32 addend@<cx:bx>);

And then it gives me this output:

Hope you enjoyed this, happy reversing!